QUTCC🤗: Quantile Uncertainty Training and Conformal Calibration for Imaging Inverse Problems
Cassandra Tong Ye, Shamus Li, Tyler King, Kristina Monakhova
Abstract
Quantile Regression: Pinball Loss
Quantile regression is a general approach to estimate the conditional quantiles of a target distribution rather than the mean of a response variable. This is often accomplished by leveraging an asymmetric loss function, called pinball loss, tailored to the specified quantile level.
where q ∈ (0,1) is the desired quantile level, x is the true value, and x̂ is the predicted value. This asymmetric penalty ensures that overestimation and underestimation are weighted differently according to the target quantile. For example, if q = 0.1, then overestimates will be penalized heavier than underestimates.
Pinball loss has been used in the past to predict a fixed set of upper and lower confidence bounds (Im2Im-UQ). In contrast, our work investigates learning the full spectrum of quantiles, commonly referred to as Simultaneous Quantile Regression (SQR) , for imaging inverse problems.
Our Method: QUTCC
We propose QUTCC (pronounced: CUTESY🤗), short for Quantile Uncertainty Training and Conformal Calibration, a novel method for simultaneous quantile prediction and conformal calibration that enables efficient and accurate uncertainty quantification for imaging inverse problems. QUTCC uses a single neural network to estimate a distribution of quantiles. During the conformal calibration step, QUTCC applies a non-uniform, nonlinear scaling to the uncertainty bounds, compared to constant scaling used by prior methods. This results in smaller and potentially more informative uncertainty intervals. Additionally, because all quantiles are learned during training, QUTCC can query the full quantile range at inference time to construct a pixel-wise estimate of the underlying probability distribution.

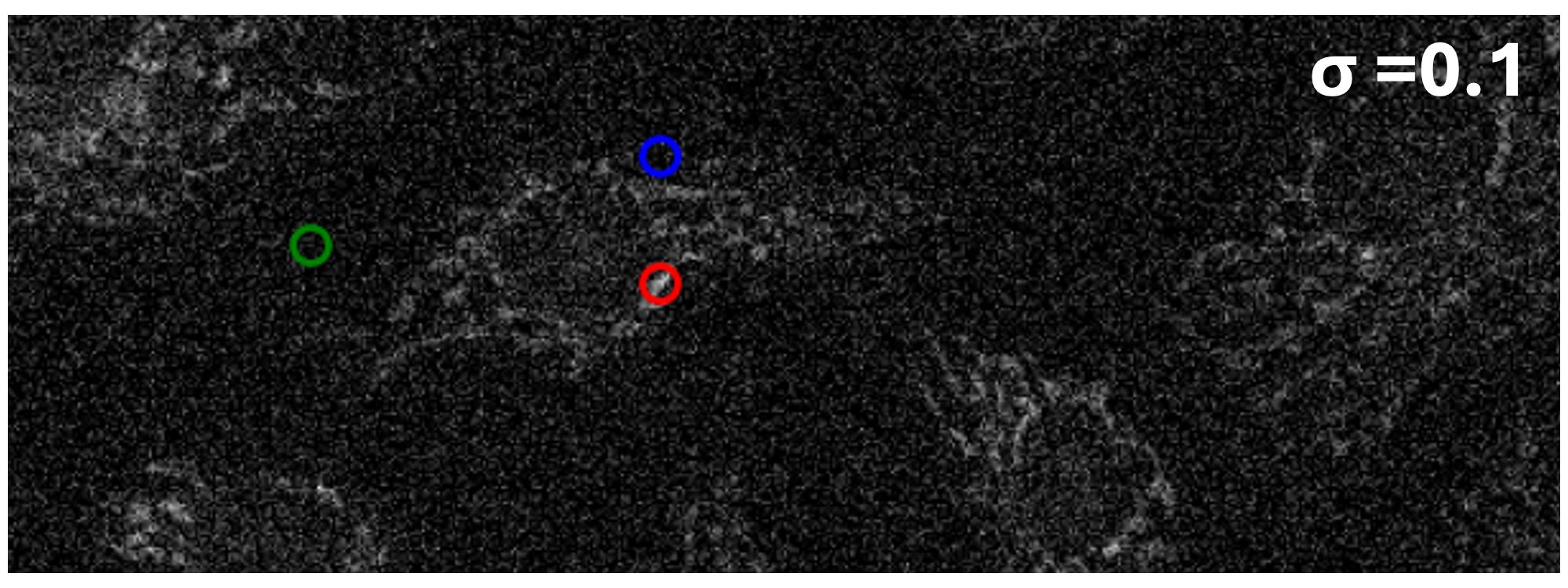
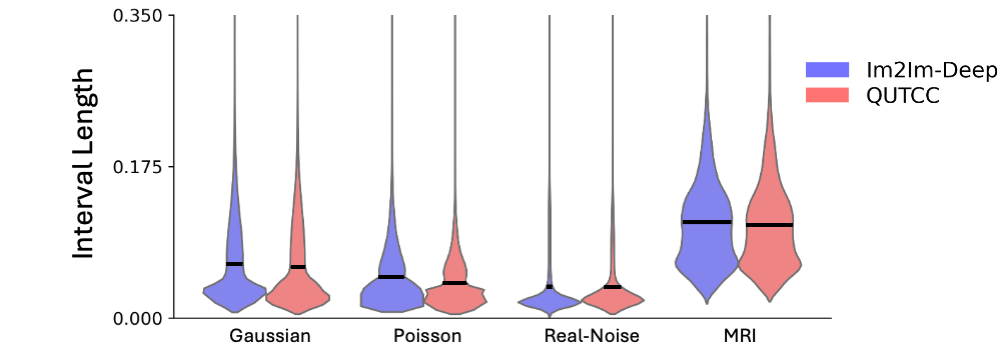
QUTCC Produces Smaller Uncertainty Intervals

Pixel-wise Probability Density Functions